Building a Regular Expression Parser From Scratch
I decided early on that I was going to build the compiler for my shader language entirely from scratch, without using off-the-shelf tools or libraries. My reasons for doing this warrant a post of their own, but suffice to say, building things the hard way brings me a deep satisfaction. One of the first steps was to establish a flexible way to identify tokens in the input. And that’s how, instead of writing a parser for the language I had designed, I found myself writing a parser for regular expressions.
Note: If you’re looking for an informal overview of how you might implement a regular expression parser, this article is for you! If you’d rather explore some real code than read my commentary, look here.
Some Light Theory
Regular expressions can be implemented with just three operations: concatenation, unions, and the Kleene star. However, to more conveniently and legibly define patterns, I also wanted to support non-capturing groups for associativity, character classes with ranges, and the Kleene star’s cousins, ? and + (zero-or-one and one-or-more, respectively).
I was familiar with a Go package called nex that also implements a regular expression parser, and it turned out to be an extremely helpful reference. If you trace the nex parsers’s web of recursive function calls, the underlying state machine looks something like this:
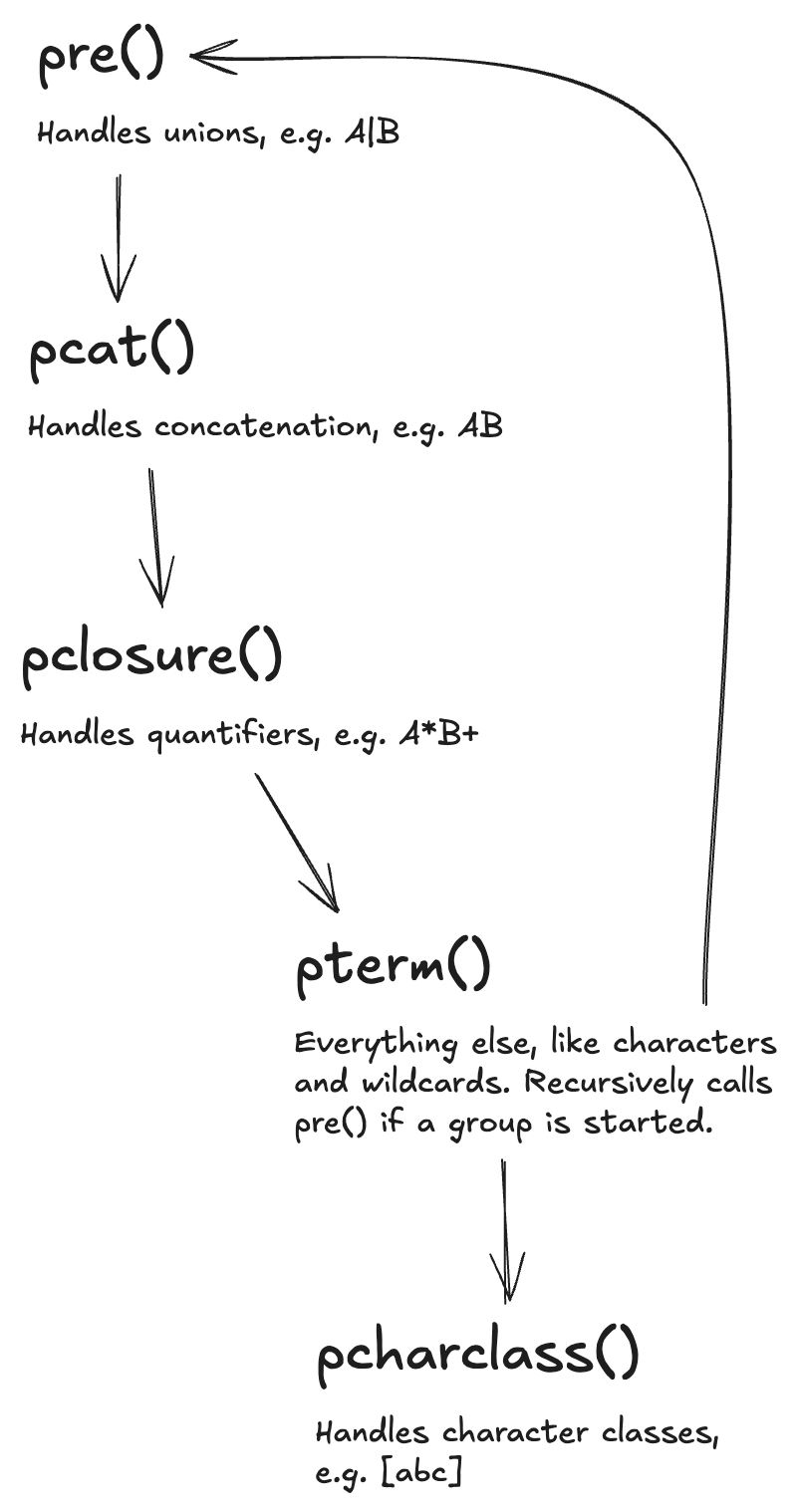
As an aside, the paper that inspired nex, Structural Regular Expressions by Rob Pike, is a quick and fantastic read.
This isn’t a complete state machine - there are no transition conditions, and the transitions traveling back up the call stack are implicit. I’m sure there is a more formal way to present the same state machine as a push-down automaton - after all, a recursive descent parser is also a state machine with a stack. But, practically speaking, this representation is good enough to start writing some code against. And, in my opinion, using recursion to pass information through the call stack is most intuitive.
Parse Tree Representation
With the basic flow of the parser outlined, the next logical step is to define a data structure to represent the parsed regular expression. We could skip this step and build an NFA directly within the parser, but I like using an intermediate representation to separate the concerns a bit more cleanly. Regular expressions can be represented as trees, like this:
type NodeKind int
const (
Literal NodeKind = iota
Wildcard
Range
Concat
Union
Maybe
ZeroPlus
OnePlus
)
type Node struct {
Kind NodeKind
Left *Node // All operator kinds use this
Right *Node // Binary operator kinds use this
Val rune // Value kinds use this
}
Note: In Go, we might instead implement this with interfaces and type switches, but my intention is to provide highly readable examples that can be implemented in any language.
You may notice that non-capturing groups and character classes are not directly represented. But, they don’t need to be! Groups exist to express associativity, which means they can be encoded into the structure of the tree itself. And, character classes are just fancy unions. As an example, here’s how a parse tree could look for the pattern f[0-9]*(\.[0-9]+)?|NaN.
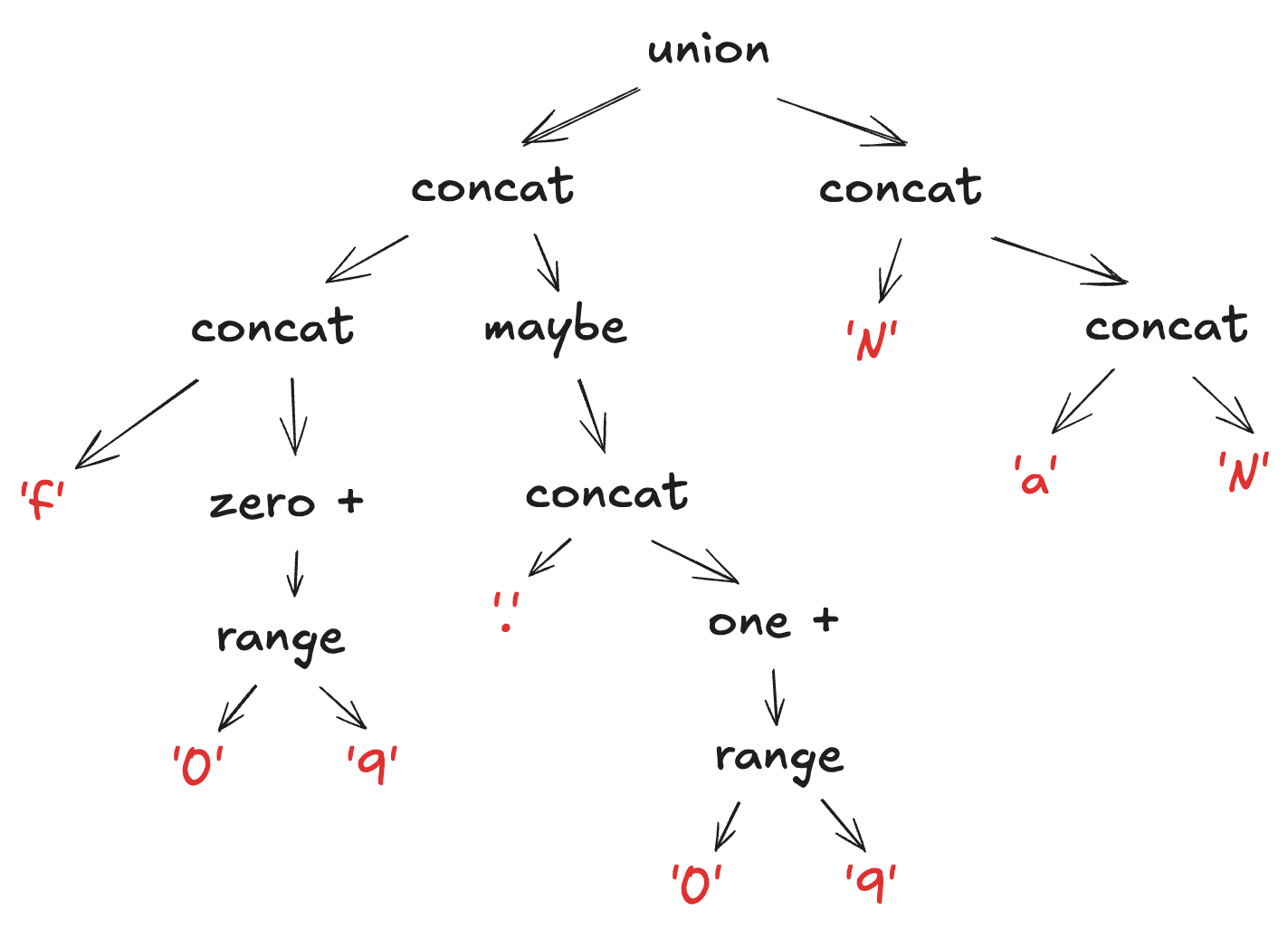
Implementing The Parser
Finally, combining the intermediate representation with the state machine from before leads us to the implementation below. Some details, like handling invalid input, have been omitted for brevity, but a complete implementation in C++ can be found here.
// peek() and consume() are functions used to inspect the
// current rune in the input and conditionally advance to the
// next rune in the input, respectively.
func parseUnion() *Node {
tree := parseConcat()
for consume('|') {
tree = &Node{
Kind: Union,
Left: tree,
Right: parseConcat(),
}
}
return tree
}
func parseConcat() *Node {
tree := parseQuant()
// Concatenation doesn't have its own operator symbol - it's
// implied whenever two values are adjacent. Because groups
// and unions are the only things higher in the call stack,
// we can assume concatenation as long as the current rune
// doesn't continue a union or close a group.
for peek() != 0 && peek() != '|' && peek() != ')' {
tree = &Node{
Kind: Concat,
Left: tree,
Right: parseQuant(),
}
}
return tree
}
func parseQuant() *Node {
tree := parseValue()
switch peek() {
case '?':
tree = &Node{Kind: Maybe, Left: tree}
consume('?')
case '+':
tree = &Node{Kind: OnePlus, Left: tree}
consume('+')
case '*':
tree = &Node{Kind: ZeroPlus, Left: tree}
consume('*')
}
return tree
}
func parseValue() *Node {
switch peek() {
case '(':
return parseGroup()
case '[':
return parseClass()
default:
return parseLit()
}
}
// We can think about groups as starting a new instance of the
// state machine, consuming only the input between parentheses,
// so we call parseUnion unconditionally.
func parseGroup() *Node {
consume('(')
tree := parseUnion()
consume(')')
return tree
}
// parseEscape has been left as an exercise for the reader.
// Once you've enumerated valid escape sequences, it's fairly
// straightforward. As an additional challenge, how might we
// implement special escape sequences, like \s to match all
// whitespace characters?
func parseLit() *Node {
switch peek() {
case '\\':
return parseEscape()
case '.':
tree := &Node{Kind: Wildcard}
consume('.')
return tree
default:
tree := &Node{Kind: Literal, Val: peek()}
consume(peek())
return tree
}
}
func parseClass() *Node {
consume('[')
tree := parseRange()
for !consume(']') {
tree = &Node{
Kind: Union,
Left: tree,
Right: parseRange(),
}
}
return tree
}
// parseClassLit has also been left as an exercise for the
// reader. The important bit is that we can't simply call
// parseLit because characters within classes follow different
// rules.
func parseRange() *Node {
tree := parseClassLit()
if consume('-') {
tree = &Node{
Kind: Range,
Left: tree,
Right: parseClassLit(),
}
}
return tree
}